Olá!
Enquanto fazia algumas configurações nesse site, tive uma ideia interessante.
Com o jekyll, no arquivo de configuração é preciso informar qual é o idioma do blog.
JoaoVCMiranda.github.io/_config.yml
yml
# The Site Configuration
# Import the theme
theme: jekyll-theme-chirpy
# The language of the webpage › http://www.lingoes.net/en/translator/langcode.htm
# If it has the same name as one of the files in folder `_data/locales`, the layout language will also be changed,
# otherwise, the layout language will use the default value of 'en'.
lang: en
Ideia
Antes de pesquisar como fazer para identificar o idioma de cada postagem,me perguntei qual seria a divergência KL(Kullback-Leibler) ou Entropia Relativa entre as duas postagens.
Que é uma medida de ineficiência na codificação de uma mensagem supondo uma distribuição quando na verdade é outra.
Como assim ? O idioma é composto por um alfabeto de várias letras, porém, a distribuição dessas não é uniforme! Por exemplo: É mais provável encontrar uma vogal que uma consoante específica qualquer em português ou encontrar a letra "y" em inglês do que em português.
Dessa forma, de acordo com a frequência relativa de cada caractere no idioma, podemos inferir e, portanto, codificar mensagens com menos bits se já soubermos previamente qual o idioma.
Para bom entendedor meia palavra bas��
No ditado popular acima, é possível codificar a mensagem com dois caracteres a menos de modo que para falantes nativos de português.
E de conhecimento do contexto, veja se ainda é possível compreender a frase omitindo todas as vogais
P�r� b�m �nt�nd�d�r m��� p�l�vr� b�st�
Entropia Relativa
Dessa forma, podemos considerar que toda mensagem escrita em um idioma(português) tem uma distribuição de "massa" de caracteres $ p $.
Então podemos considerar que uma mensagem em português é um vetor P e que cada elemento é uma variável aleatória com distribuição $ p $
Já uma mensagem em inglês E teria uma outra distribuição de caracteres $ e $
Assim, dadas as distribuições de caracteres
$$
p:\rho \rightarrow 0,1
$$
$$
e:\varepsilon \rightarrow 0,1
$$
$$
D(p||e) = \sum_{x \in \rho} p(x)log\Bigl(\frac{ p(x) }{ e(x) }\Bigr)
$$
Atenção: todos $ \log $ aqui representados referem-se ao $\log_2$, cuja a unidade é bits e não precisa ser um número inteiro!
Onde $ \rho $ e $ \varepsilon $ são os conjuntos dos caracteres de cada idioma, por definição se uma letra não está no alfabeto, então a probabilidade dessa aparecer na mensagem é 0.
Se uma letra do alfabeto de $ p $ não está em $ e $.
$$ \lim_{e->0^{+}} p \ log\Bigl(\frac{ p }{ e }\Bigr) = +\infty $$
Se uma letra do alfabeto de $ e $ não está em $ p $
$$
\lim_{p->0} p \ log\Bigl(\frac{ p }{ e }\Bigr) = 0
$$
E isso basta como justificativa do porquê a divergência KL não ser uma métrica de verdade, já que:
$$
D(p||e) \ne D(e||p)
$$
Além de outros detalhes como não obedecer a desigualdade triangular.
Mas a distância só é 0 quando $e=p \ \forall x$
Porém, ainda assim é um dos elementos mais legais da teoria de informação!(Veja os próximos tópicos!)
Para simplificar a notação, ao invés de usar $ p_(y) $ para representar uma distribuição de probabilidade para uma variável aleatória $ Y $, omitirei o Y para $ p(y) $ que significa:
$$ p(y) = Pr{Y=y} $$
Sendo assim, $ p(x) $ não é necessariamente igual a $ p(y) $ quando $ x=y $ pois são distribuições diferentes.
Informação Mútua
A informação mútua de duas variáveis aleatórias é a seguinte ideia:
Inicialmente, todas a a informação que sabemos sobre uma certa variável aleatória Y é a sua distribuição de probabilidades. E o mesmo vale para uma outra variável aleatória X, se essas variáveis forem independentes entre si, então o conhecimento do valor de uma em nada afeta o conhecimento da outra.
Mas as coisas ficam mais interessantes se elas forem correlacionadas.
Suponha agora que X é uma mensagem que atravessa um canal e o valor recebido (com erros) é Y, se soubermos qual é a distribuição de X e Y previamente, podemos corrigir os erros que surgirem!
Com alguns códigos inteligentes é possível fazer o erro arbitrariamente pequeno sob a penalidade de adicionar redundância à mensagem
Assim, sendo Y conhecido e ambas as distribuições, é possível ter uma redução na ignorância de X e fazer uma melhor estimativa do que a mensagem orginal deve ser.
Como isso é relacionado com a Entropia Relativa ?
Dado que sabemos qual é a distribuição de X (ex:X está em português), e ao receber Y podemos calcular qual é a sua distribuição.
Sendo $ p(x,y) $ a distribuição conjunta das duas v.a.,
$ p(x,y) = p(y)p(x|y) $
Para calcular $ p(x|y)$ é preciso saber por qual tipo de canal a mensagem está sendo transmitida. Ex: BSC(Binary Symmetric Channel)
E $ p(x)p(y) $ considerando X e Y independentes.
teremos assim, duas novas variáveis aleatórias que seguem a essas distribuições.
Então, a Informação Mútua, é a distância entre o que saberíamos caso as variáveis fossem independentes e o que sabemos sobre Y e o canal. Ou seja, é a redução de "ignorância" de X, sabendo Y.
$$
I(X;Y) = D(p(x,y)||p(x)p(y)) = \sum_{x,y} \ p(x,y)\ \log \Bigl(\frac{p(x,y)}{p(x)p(y)} \Bigr)
$$
Entropia
E por último, mas não menos importante, surpreendentemente a entropia também pode ser definida a partir da divergência KL.
A entropia em teoria de informação foi um conceito introduzido em teoria de informação devido ao fato de já existir uma definição muito parecida em Termodinâmica, que está relacionada ao "grau de desorganização das moléculas" que também pode ser pensada como a quantidade de "informação" ou "bits" necessários para representar o sistema.
Essa é uma representação que mescla ambos os conceitos tanto em Termodinâmica como em T.I.
Assim, seria a informação que uma única v.a. carrega. Por isso também é chamada de Informação-própria.
$$
I(X,X) = \sum_{x,x} p(x)log\Bigl( \frac{p(x,x)}{p(x)p(x)}\Bigr) \implies \sum_{x,\cancel{x}}p(x, \cancel{x})\ log\Bigl( \frac{\cancel{p(x)}\cancel{p(x|x)}^{1}}{\cancel{p(x)}p(x)}\Bigr)
$$
Desculpe pelos cancelamentos grosseiros... Esse da distribuição conjunta foi uma marginalização... E o elemento dentro do log pode ser considerado constante no somatório interno após simplificar a fração
Assim, a definição de entropia, seria a quantidade de "dígitos" mínima, em média, para representar a v.a., ou como é definido em 1
"É o valor esperado ( $ E_p $ ) da v.a. $\boxed{-\log(p(x))}$"
Que é mais acurado, pois a primeira "definição" que comentei só vale como quantidade de dígitos, quando é uma v.a. binária
Ao que interessa, como calcular ?
Deixei esses arquivos aqui no site mesmo em assets/posts/20240416/, removi previamente as expressões em MathJax, para não complicar mais os intervalos de caracteres que vou selecionar no unicode.
kl.py
py
import math
def char_dist(arq):
# Modelo de distribuição
D = [0]*(ord('Z')-ord('A') + ord('z')-ord('a') + ord('ƿ')-ord('À'))
# Leitura do arquivo
with open(arq, 'r') as p:
for x,line in enumerate(p):
for y,c in enumerate(line):
# Capital
if ('A'<=c<='Z'):
D[ord(c)-ord('A')]+=1
# Lowercase
if('a'<=c<='z'):
D[ord('Z')-ord('A')+1 +ord(c)-ord('a')]+=1
# Latim Extended + European Latim
if('À'<=c<='ƿ'):
D[ord('Z')-ord('A')+1+ord('z')-ord('a')+1 +ord(c)-ord('À')]+=1
# Normalização
cte = sum(D)
for i,x in enumerate(D):
D[i] = x/cte
return D
def entropia_relativa(Q,R):
er = 0
for i,q in enumerate(Q):
if(q==0):
er += 0
elif(R[i]!=0):
er += q*math.log2(q/R[i])
else:
return math.inf
return er
if __name__ == "__main__":
P = char_dist('P.txt')
E = char_dist('E.txt')
print('D(P||E)=', entropia_relativa(P, E), 'bits')
print('D(E||P)=', entropia_relativa(E, P), 'bits')
{: file=""}
Porém,
o que eu não esperava, é que nas minhas 41 linhas escritas em português poderiam não haver incidências de letras comuns no inglês como por exemplo: "H"(maiúsculo) e algo parecido ter acontecido com o inglês.
bash
$ python kl.py
D(P||E)= inf bits
D(E||P)= inf bits
E isso pode ser explicado com a ajuda do histograma abaixo
Histogramas
 {:.dark .w-100}
{:.dark .w-100}
 {:.light .w-100}
Histograma das distribuições
{:.light .w-100}
Histograma das distribuições
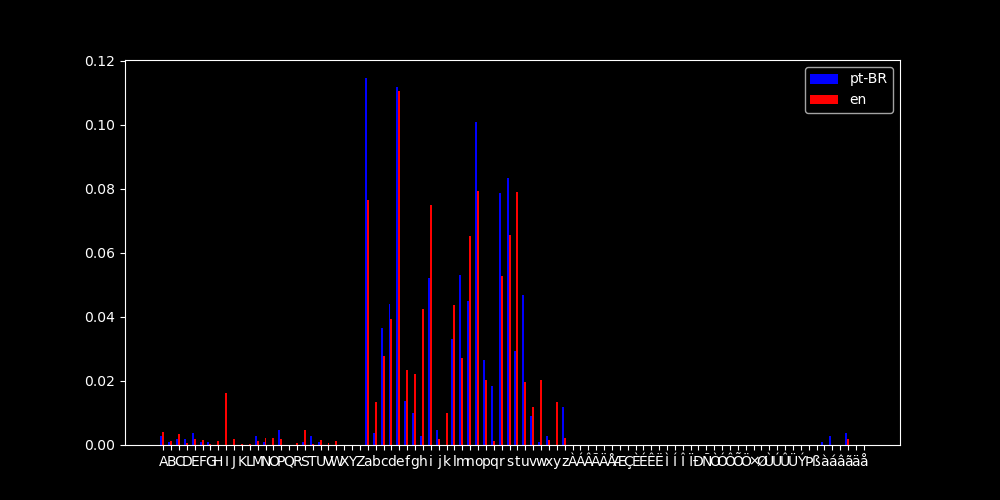
Muito bem, talvez eu tenha exagerado no intervalo... Por isso irei limitá-lo até a última incidência de caracteres.
 {:.dark .w-100}
{:.dark .w-100}
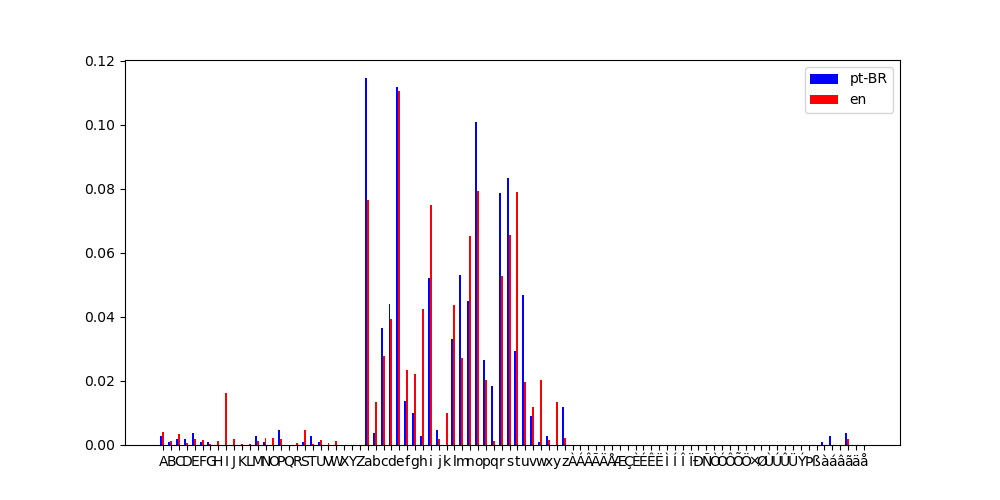 {:.light .w-100}
Histograma das distribuições
{:.light .w-100}
Histograma das distribuições
E possível compreender melhor porquê que as distribuições estão "inifinitamente" distantes, pois há caracteres normalmente utilizados em português que eu não utilizei em minhas linhas, e vice-versa!
Sobre os ombros de gigantes
Porém, como eu gostaria de efetivamente chegar a algum valor de entropia, resolvi pesquisar clássicos da literatura portuguesa e inglesa. E assim, encontrei os seguintes livros(de domínio público):
A Pata da Gazela (1870) por José de Alencar
É um triângulo amoroso entre Amélia, Leopoldo e Horácio. Mas o climax desse romance é o mistério é envolvido pelos sapatinhos da moça.
5025 linhas
A Study in Scarlet (1887) por Sir Arthur Connan Doyle
É a primeira aparição dos icônicos personagens Sherlock Holmes e Dr. John Watson. Também há mistério, o estudo feito é para desvendar um assassinato.
4737 linhas
Resultados
E sem mais delongas, eis aqui a entropia relativa entre A Pata da Gazela e A Study in Scarlet
bash
$ python kl.py
D(doyle||alencar)= inf bits
D(alencar||doyle)= inf bits
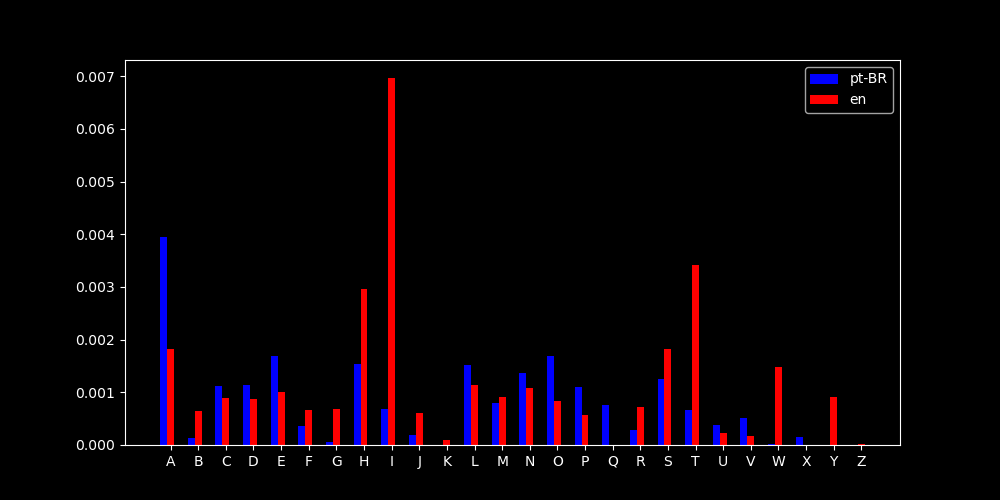
Que pode ter acontecido ? Ao inspecionar a distribuição de caracteres, percebi o seguinte...
 {:.dark .w-100}
{:.dark .w-100}
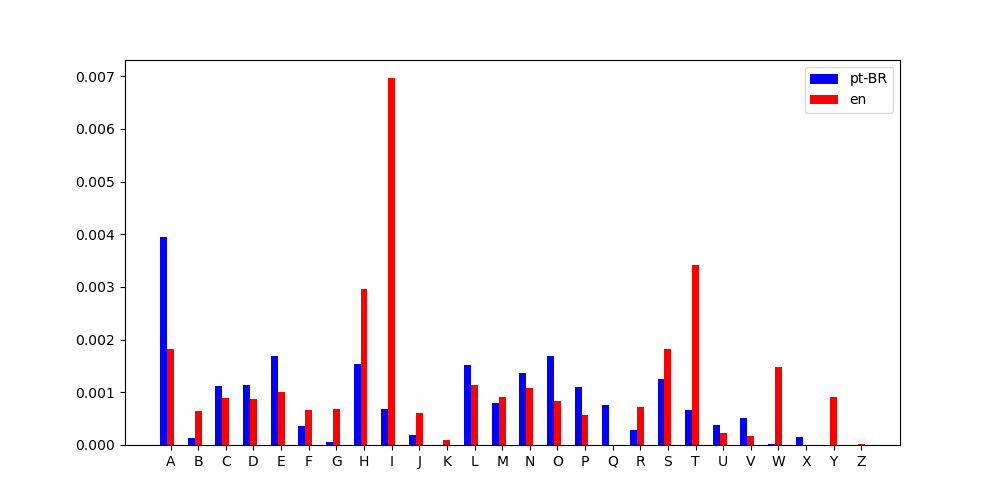 {:.light .w-100}
Histograma das distribuições
{:.light .w-100}
Histograma das distribuições
"X" só aparece em "A Pata da Gazela" e "(K, W, Y)" só aparece em "A Study in Scarlet"
Caso você esteja se perguntando onde "X" aparece em português... "Capítulo XVI..."
Até aqui eu tentei fazer com que a divergência fosse calculada mantendo os arquivos de entrada intocados.
Existem alguns pré-processamentos que posso fazer como remover os acentos das letras em português, juntar as letras maiúsculas e minúsculas. Mas acho que isso não de deixaria satisfeito já que pode não "funcionar" sempre. Bem o que fazer então ?
Unicode
Afinal como são representados os caracteres na memória do computador ? Como diferenciá-los ? O Unicode, tem a solução para os nossos problemas(ou quase).
O Unicode é como uma grande função $ U(x) $ onde x é um número em hexadecimal(base 16) que é geralmente representada da seguinte maneira:
Representação|$ U(x) $
U+0041| A
U+0061| a
Mas esse é apenas uma tabela de correlação para mapear os caracteres(code poits) aos números em hexadecimal, mas deixa aberta a codificação para os dispositivos.
Planos do unicode
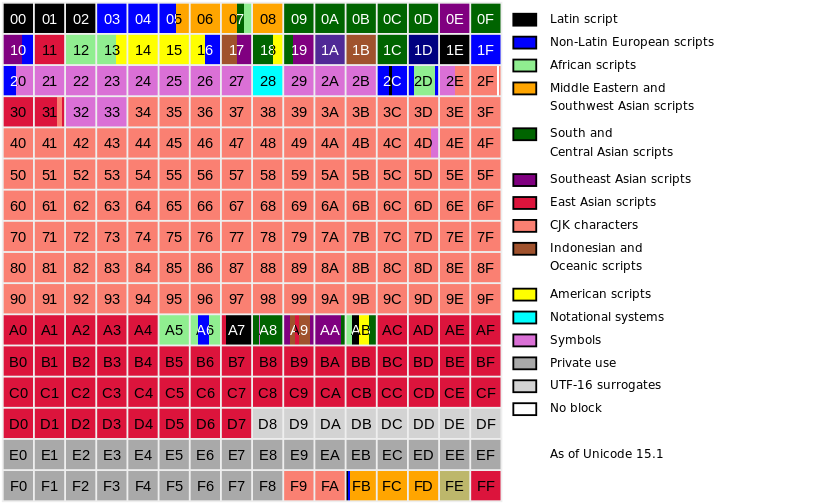
A representação de cima pertence ao plano 0 do unicode.Isto é aos primeiros $ 16^4 = 65 536 $ code points. Mas podemos adicionar um prefixo de 1-F e gerar os demais 16 planos. Tendo assim $ 1 114 112 $2 code points. Os planos 4-D ainda não foram utilizados. O que nos dá algum tempo para inventar novos caracteres para evitar que o newspeak torne-se uma realidade.
 {: .w-100}
Plano 0 do Unicode - Fonte: Wikipédia
{: .w-100}
Plano 0 do Unicode - Fonte: Wikipédia
Como podemos perceber, mal tocamos a superfície dos 3 primeiros blocos do primeiro plano.
UTF-8
Para colocar o nosso conhecimento de unicode em prática, é preciso de um sistema para codificar os code points em '0's e '1's. já, atualmente,essa é a lógica que os dispositivos eletrônicos utilizam para funcionar.
O UTF-8 é um padrão de tamanho variável para codificação de caracteres. Isso significa, que com algo entre 1 e 4 bytes, esse poderá representar qualquer caractere do unicode.
Bytes
Um byte é um conjunto de slots na memória, que contem 8 bits. Bits podem ser '0's ou '1's
Assim, tem $ 2^{4*8} = 2^{32} = 4 294 967 296 $
Curiosamente é esse também é o maior intervalo que o tipo de dado
int32suporta em c++. E que eventualmente eu esqueço
Esse número consegue ser grande até para os padrões do unicode. Mas tem um motivo. Algumas dessas posições são espaços reservados para metadados do caractere. Por isso que o tamanho da sequência é variável.
Se o seu caractere foi codificado e começa assim 0..., certamente ele terá apenas mais outros 7 bits.
Na verdade existe uma tabela para isso, quanto "depois" o caractere for adicionado ao unicode, maior a sua sequência. E, portanto, assim mais bits são necessários para representá-lo.
Onde
xpode ser 0 ou 1.
U+|Bits codificados | Nº de xU+0000, U+007F|0xxxxxxx |7
U+0080, U+07FF|110xxxxx 10xxxxxx |11
U+0800, U+FFFF|1110xxxx 10xxxxxx 10xxxxxx |16
U+010000, U+10FFFF|11110xxx 10xxxxxx 10xxxxxx 10xxxxxx |21
Assim o é possível codificar qualquer caractere dos 10 primeiros planos do Unicode com UTF-8.
Contudo, há um custo... Quando o Unicode foi criado, já existia um sistema de codificação, o ASCII e ele foi criado para ser retrocompatível com esse. Assim, os primeiro caracteres, representados de U+0000 até U+007F, são precisamente os caracteres do ASCII.
Por isso, ao gerar os texto em ascii, esses consomem menos espaço que os demais.
bash
$ cat ascii.txt
Lorem ipsum dolor sit amet, consectetur adipiscing elit,....
$ du -b ascii.txt
4123 ascii.txt
Agora veja o que acontece quando trocamos todas as letras "o" por "ó"
bash
$ cat utf.txt
Lórem ipsum dólór sit amet, cónsectetur adipiscing elit, ....
$ du -b utf.txt
4285 utf.txt
Custou precisamente um byte por cada "ó" adicionado.
Armazenamento, atualmente é um dos recursos mais "baratos" na computação(em relação ao processamento e ao tempo) então não é um grande problema.
Mas pensando nos países africanos e asiáticos, escrever no idioma desses é 3 vezes mais "pesado" para armazenar. Veja o que acontece se substituirmos todos os caracteres do nosso arquivo para japonês
bash
$ cat utf2.txt
ゴゴゴゴゴゴゴゴゴゴゴゴゴゴゴゴゴゴ...
$ du -b utf2.txt
11892 utf2.txt
Que é quase o triplo(Só não foi pois não substitui a pontuação)
Implementando ao código
Para gerar a nossa estimada distribuição binária.
python
def bin_dist(arq):
D = [0,0]
with open(arq, 'r') as p:
for x,line in enumerate(p):
for y,c in enumerate(line):
# Capital + Lowercase
if (('a'<=c<='z') or ('A'<=c<='Z')):
# 0xxxxxxx
D[0]+=1
for x in format(ord(c),'b'):
if(x == '0'):
D[0]+=1
else:
D[1]+=1
# Latim Extended + European Latim
if ('À'<=c<='ƿ'):
# 110xxxxx 10xxxxxx
b = format(ord(c), 'b')
D[0]+=2 + (11 - len(b))
D[1]+=3
for x in format(ord(c),'b'):
if(x == '0'):
D[0]+=1
else:
D[1]+=1
# Normalização
cte = sum(D)
for i,x in enumerate(D):
D[i] = x/cte
return D
{: file="kl.py"}
Resultado Final
Finalmente, podemos calcular qual é de fato a divergência-kl entre os livros de José de Alencar e Sir Arthur Connan Doyle.
python
if __name__ == "__main__":
P = bin_dist('P.txt')
E = bin_dist('E.txt')
doyle = bin_dist('scarlet.txt')
alencar = bin_dist('gazela.txt')
print('D(P||E)=', entropia_relativa(P, E), 'bits')
print('D(E||P)=', entropia_relativa(E, P), 'bits')
print('D(doyle||alencar)=', entropia_relativa(doyle, alencar), 'bits')
print('D(alencar||doyle)=', entropia_relativa(alencar, doyle), 'bits')
print(doyle, alencar)
bash
$ python kl.py
D(P||E)= 7.504684431210509e-05 bits
D(E||P)= 7.507532171208055e-05 bits
D(doyle||alencar)= 1.9159800574827714e-06 bits
D(alencar||doyle)= 1.915881083528522e-06 bits
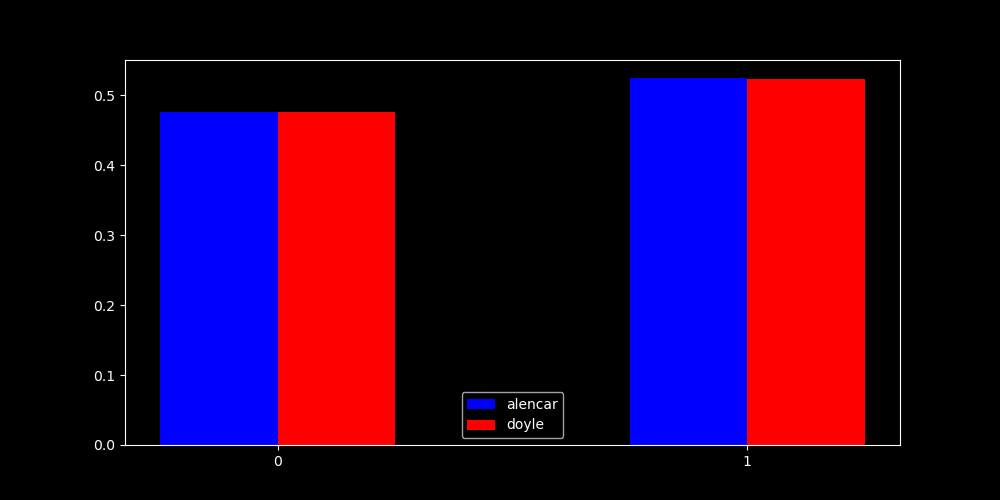
[0.4766607641124705, 0.5233392358875295] [0.4758468150403702, 0.5241531849596298]
 {:.dark .w-100}
{:.dark .w-100}
 {:.light .w-100}
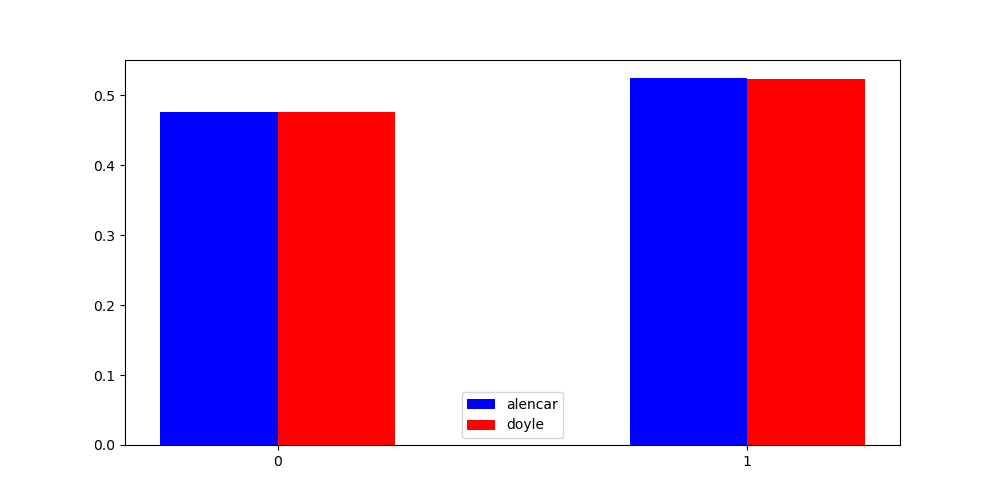
Histograma das distribuições
{:.light .w-100}
Histograma das distribuições
Esses resultados significam que caso fossemos fazer um código ótimo para representar os caracteres em um idioma quando na verdade é o outro, se fossemos fazer um código de Huffman o comprimento médio por bit seria aproximadamente $ 7.5*10e-5 $ maior, ou seja, que a cada 100.000 caracteres, 7.5 bits poderiam ser "economizados".
Acho que a conclusão não é tão surpreendente, mas serviram muito bem para treinar algumas habilidades e explorar a curiosidade.
Se você chegou até aqui comigo, muito obrigado!!!
Esse é uma das postagens que faço durante o meu processo de aprendizado também. Então me desculpe por eventuais falhas, ou por postergar demais o resultado. Foi uma longa jornada, mas valeu a pena.
Até que o unicode não é tão ruim para as liguas latinas, quem sabe no futuro não se torne a codificação ótima para todos os idiomas no mundo, simultanea e dinamicamente ou quem sabe os supercomputadores resolvam isso colocando todos os caracteres que existem, ou vão existir, em estado de superposição.
Desse modo, quem sabe sabe as pessoas se comuniquem melhor. É o objetivo.